https://arxiv.org/abs/1907.00503
Modeling Tabular data using Conditional GAN
Modeling the probability distribution of rows in tabular data and generating realistic synthetic data is a non-trivial task. Tabular data usually contains a mix of discrete and continuous columns. Continuous columns may have multiple modes whereas discrete
arxiv.org
0. Abstract
- 표 형식 데이터는 이산형과 연속형 특성이 혼합되어 있으며, 연속형은 다봉 분포를 가질 수 있고 이산형은 클래스 불균형 문제가 있어 모델링이 어렵다.
- 기존의 통계적 방법이나 신경망 기반 생성 모델은 이러한 구조를 제대로 학습하지 못하는 경우가 많다.
- CTGAN은 조건부 생성기(Conditional Generator)를 활용하여 이산형 불균형 및 다봉 연속형 특성 문제를 해결하도록 설계되었다.
- 7개의 시뮬레이션 데이터와 8개의 실제 데이터를 포함한 벤치마크 실험에서 CTGAN은 대부분의 실제 데이터셋에서 베이지안 네트워크 기반 방법보다 더 나은 성능을 보였다.
1. Introduction
최근 딥 생성 모델의 발전으로 이미지와 텍스트를 기반으로 한 확률 분포 학습과 고품질 샘플 생성이 가능해졌다. 특히 지난 2년간, tabular data 생성을 위한 GAN(생성적 적대 신경망) 기술이 활발히 개발되었으나 기존 통계적 방법보다 분포 모델링에 유연성을 가지는 반면, 평가 기준 마련이 필요했다. 이에 실제 데이터셋을 활용한 벤치마킹 시스템을 구축하고 최신 GAN 기법 3가지를 테스트했으며, Bayesian networks를 기반으로 한 2개의 baseline 모델과 비교했다. 실험 결과, tabular data 특유의 이산형과 연속형 컬럼 동시 모델링, 다중 모드의 비가우시안 연속 값, 심각한 범주형 불균형 등의 문제로 인해 GAN들이 일부 평가 지표에서 baseline 모델에 미치지 못하는 한계가 확인되었다.
이를 해결하기 위해 본 논문에서는 CTGAN(conditional tabular GAN)을 제안하며, 주요 기법은 다음과 같다:
- 모드별 정규화를 통한 학습 절차 보강
- 모델 구조 변경
- 조건부 생성기 및 샘플링 기반 학습으로 데이터 불균형 처리

CTGAN은 동일한 데이터셋 벤치마크에서 기존 베이지안 네트워크 및 다른 GAN들보다 월등한 성능을 보였다. 논문의 기여는 다음과 같다:
- 합성 데이터 생성을 위한 Conditional GANs
- Tabular 데이터 생성을 위한 CTGAN을 제안
- 기존 방법들보다 전반적으로 더 우수한 성능을 보이며, 전체 데이터셋 중 87.5% 이상에서 Bayesian networks를 능가
- 성능 검증을 위해 TVAE (Tabular VAE)라는 VAE 기반 모델도 설계하여 비교
- TVAE는 데이터 자체를 생성기에 직접 활용하지만, 그럼에도 불구하고 CTGAN이 3개 데이터셋에서 더 좋은 성능을 보임
- 합성 데이터 생성 알고리즘을 위한 벤치마킹 시스템
- 다양한 tabular 데이터셋, 평가지표, baselines, 최신 기법들을 포함하는 벤치마킹 프레임워크 설계
- 벤치마크에는 현재 기준으로 다음이 포함됨:
- 5개의 deep learning 기반 방법, 2개의 Bayesian network 방법, 15개의 tabular 데이터셋, 2개의 평가 메커니즘
2. Related Work
지난 10년간 합성 데이터 생성은 테이블의 각 컬럼을 확률 변수로 보고 전체 데이터를 하나의 다변량 확률 분포(joint multivariate probability distribution)로 모델링한 뒤, 이로부터 샘플링하는 방식으로 이루어졌다. 대표적으로 decision tree, Bayesian network, copula, spatial decomposition tree 등이 사용되었으나, 분포 제약과 계산 복잡도 문제로 인해 데이터 정밀도(fidelity)가 낮다는 한계가 있었다.
이후 VAE, GAN 및 그 다양한 확장 모델들이 등장하면서 표현력과 유연성 면에서 기존 방법보다 우수한 대안으로 주목받았다. 특히 의료 데이터 생성 분야에서 GAN 기반 모델들이 다양하게 활용되었다:
- medGAN: autoencoder + GAN을 결합하여 이진 및 연속형 비시간 데이터 생성
- ehrGAN: 의료기록 증강
- tableGAN: CNN 기반, label column의 품질 최적화 → 분류기 학습용 데이터 생성 가능
- PATE-GAN: differential privacy를 보장하는 합성 데이터 생성
- 그 외 시간 시계열 또는 이산형 테이블 데이터 생성 모델도 존재
3. Challenges with GANs in Tabular Data Generation Task
합성 데이터 생성은 테이블 \( T \) 로부터 학습된 생성기 \( G \) 를 이용해 새로운 합성 테이블 \( T_{\text{syn}} \) 을 만드는 과정이다.
테이블 \( T \) 는 다음과 같이 구성된다:
- 연속형 컬럼 집합: \( \{C_1, \dots, C_{N_c}\} \)
- 이산형 컬럼 집합: \( \{D_1, \dots, D_{N_d}\} \)
- 각 컬럼은 확률 변수이며, 전체 데이터는 결합 분포 \( P(C_{1{:}N_c}, D_{1{:}N_d}) \) 를 따름
- 하나의 데이터 행: \[ r_j = \{c_{1,j}, \dots, c_{N_c,j}, d_{1,j}, \dots, d_{N_d,j}\}, \quad j \in \{1, \dots, n\} \]
전체 테이블 \( T \) 는 학습용 \( T_{\text{train}} \) 과 테스트용 \( T_{\text{test}} \) 으로 분할된다.
생성기 \( G \) 를 \( T_{\text{train}} \) 에 대해 학습시킨 후, \( G \) 로부터 개별 행을 샘플링하여 \( T_{\text{syn}} \) 을 생성한다.
생성기의 성능 평가는 두 가지 기준으로 수행된다:
- Likelihood Fitness \[ T_{\text{syn}} \sim P(C_{1{:}N_c}, D_{1{:}N_d}) \quad \text{(분포 유사도)} \]
- Machine Learning Efficacy \[ \text{Train}(f_{\text{syn}} \text{ on } T_{\text{syn}}) \approx \text{Train}(f_{\text{real}} \text{ on } T_{\text{train}}) \]
\( \Rightarrow \) 두 모델이 \( T_{\text{test}} \) 상에서 유사한 성능을 내는지 평가
Mixed data types.
실제 데이터는 이산형과 연속형 데이터가 섞여 있어서, GAN은 두 가지를 동시에 생성하려면 softmax(범주형용)와 tanh(연속형용)를 함께 써야 한다.
Non-Gaussian distributions.
이미지와 달리 테이블 데이터의 연속형 컬럼은 비가우시안 분포를 가지기에 min-max 정규화가 그래디언트 문제를 유발할 수 있다.
Multimodal distributions.
연속형 컬럼 중 많은 경우 여러 봉우리(모드)를 가진 복잡한 분포를 가지는데, 기본 GAN은 이런 다중 모드를 잘 학습하지 못한다.
Learning from sparse one-hot-encoded vectors.
실제 데이터는 희소한 one-hot 벡터이고, GAN은 확률 분포를 생성해 이를 학습하는데, 희소성을 이용해 쉽게 진짜/가짜를 구분하는 문제가 있다.
Highly imbalanced categorical columns.
범주형 컬럼 대부분이 심하게 불균형해 GAN이 소수 클래스를 학습하기 어려워지고, 모드 붕괴 문제가 심해진다.
4. CTGAN Model
- CTGAN은 tabular data distribution을 모델링하고 그 분포에서 rows를 샘플링하는 GAN 기반 방법이다.
- 비가우시안(non-Gaussian) 및 multimodal distribution 문제를 극복하기 위해 mode-specific normalization(Section 4.2)을 도입했다.
- 불균형한 discrete columns를 처리하기 위해 conditional generator와 training-by-sampling(Section 4.3)을 설계했다.
- fully-connected networks와 여러 최신 기법을 사용해 high-quality 모델을 훈련한다.
4.1 Notations
다음과 같은 기호를 정의한다.
- \( x_1 \oplus x_2 \oplus \ldots \): 벡터 \( x_1, x_2, \ldots \)를 순서대로 이어 붙인(concatenate) 것
- \( \text{gumbel}_{\tau}(x) \): 벡터 \(x\)에 대해 파라미터 \(\tau\)를 가진 Gumbel Softmax [13]를 적용한 것
- \( \text{leaky}_{\gamma}(x) \): leaky 비율 \(\gamma\)를 가진 Leaky ReLU 활성화 함수를 \(x\)에 적용한 것
- \( \text{FC}_{u \to v}(x) \): \(u\)-차원 입력에 대해 \(v\)-차원 출력을 생성하는 선형 변환(linear transformation)을 적용한 것
또한, 다음 함수 및 기법들도 사용한다: tanh, ReLU, softmax, BN, dropout.
4.2 Mode-specific Normalization
신경망 학습에서는 이산값은 쉽게 표현되지만, 연속값은 복잡한 분포로 인해 표현이 어려워 기존에는 min-max 정규화를 사용했다.
CTGAN은 복잡한 분포를 가진 연속형 컬럼을 처리하기 위해 mode-specific normalization을 도입했다. 각 값은 모드를 나타내는 원-핫 벡터와 모드 내 값을 나타내는 스칼라로 구성되며, 전체 과정은 세 단계로 이루어진다.

- 각 연속형 컬럼 \( C_i \)에 대해, 변분 가우시안 혼합 모델(VGM, Variational Gaussian Mixture Model)을 사용하여 모드의 수 \( m_i \)를 추정하고 가우시안 혼합 모델을 적합시킨다.
학습된 가우시안 혼합 모델은 다음과 같다:
\[ P_{C_i}(c_{i,j}) = \sum_{k=1}^{3} \mu_k \cdot \mathcal{N}(c_{i,j}; \eta_k, \phi_k) \]
여기서 \( \mu_k \)와 \( \phi_k \)는 각각 모드의 가중치와 표준편차. - 컬럼 \( C_i \)의 각 값 \( c_{i,j} \)에 대해, \( c_{i,j} \)가 각 모드로부터 나올 확률을 계산한다. 확률 밀도는 다음과 같이 계산된다: \[ \rho_k = \mu_k \cdot \mathcal{N}(c_{i,j}; \eta_k, \phi_k) \]
- 주어진 확률 밀도로부터 하나의 모드를 샘플링하고, 샘플링된 모드를 사용해 값을 정규화한다. 그런 다음 \( c_{i,j} \)는 다음과 같이 표현된다:
- 모드를 나타내는 원-핫 벡터: \( \beta_{i,j} = [0, 0, 1] \)
- 모드 내 값을 나타내는 스칼라: \[ \alpha_{i,j} = \frac{c_{i,j} - \eta_3}{4\phi_3} \]
행 하나의 표현은 연속형 및 이산형 컬럼들의 연결(concatenation)으로 구성된다:
\[ r_j = \alpha_{1,j} \oplus \beta_{1,j} \oplus \cdots \oplus \alpha_{N_c,j} \oplus \beta_{N_c,j} \oplus d_{1,j} \oplus \cdots \oplus d_{N_d,j} \]
여기서 \( d_{i,j} \)는 이산값의 원-핫 표현(one-hot representation).
4.3 Conditional Generator and Training-by-Sampling
전통적인 GAN은 generator에 표준 다변량 정규분포(MVN, multivariate normal distribution)에서 샘플링된 벡터를 입력으로 사용하며, discriminator와 함께 학습을 통해 실제 데이터 분포를 모사한다. 그러나 이 구조는 categorical columns의 class imbalance 문제를 제대로 다루지 못한다. 소수 범주에 해당하는 데이터는 학습 중 무작위로 선택될 확률이 낮기 때문에 충분히 학습되지 않고, 반대로 데이터를 resample하면 실제 분포에서 벗어나게 된다.
이 문제는 단순한 클래스 불균형 문제보다 복잡한데, 그 이유는 다음과 같다:
- 복수의 discrete columns이 존재함
- real data distribution을 유지해야 함
이를 해결하기 위해 논문에서는 학습 시에는 각 범주가 고르게 선택되도록 하되, 생성된 샘플은 특정 범주 조건하에서의 conditional distribution을 따르도록 설계한다. 즉, generator는 다음과 같은 조건부 분포를 모델링한다:
\[ \hat{r} \sim P_G(\text{row} \mid D_{i^*} = k^*) \]
이 방식에 따라 generator는 conditional generator, 전체 GAN 구조는 conditional GAN으로 부른다.
조건부 생성기(Conditional Generator)를 GAN 구조에 통합하려면 다음의 문제들을 다루어야 한다:
- 조건(Condition)을 위한 표현(Representation)을 고안하고, 이를 위한 입력을 준비해야 한다.
- 생성된 행(Generated Rows)이 주어진 조건을 그대로 유지해야 한다.
- 조건부 생성기(Conditional Generator)가 실제 데이터의 조건부 분포(Real Data Conditional Distribution)를 학습해야 한다. 즉, \( P_G(\text{row} \mid D_{i^*} = k^*) = P(\text{row} \mid D_{i^*} = k^*) \)를 만족해야 하며, 이를 통해 원래의 분포를 다음과 같이 복원할 수 있어야 한다:
\[ P(\text{row}) = \sum_{k \in D_{i^*}} P_G(\text{row} \mid D_{i^*} = k^*) P(D_{i^*} = k) \]
우리는 이 문제를 해결하기 위해 다음의 세 가지 핵심 요소로 구성된 솔루션을 제시한다:
- Conditional Vector
- Generator Loss
- Training-by-Sampling Method
Conditional vector.
우리는 조건 \((D_{i^*} = k^*)\) 을 표현하기 위해 벡터 `cond`를 정의하며, 각 이산형 컬럼 \(D_1, \dots, D_{N_d}\)은 one-hot 벡터 \(d_1, \dots, d_{N_d}\)로 표현된다.
- 각 이산형 컬럼 \( D_i\)는 one-hot 벡터 \( d_i = [d_i^{(k)}], \quad k = 1, \dots, |D_i| \) 로 표현됨
- 여기에 대응하는 마스크 벡터는 \( m_i = [m_i^{(k)}], \quad k = 1, \dots, |D_i| \)
- 마스크는 \( i = i^* \) 이고 \( k = k^* \) 일 때만 1, 그 외는 0
- 조건 벡터는 \( \text{cond} = m_1 \oplus m_2 \oplus \cdots \oplus m_{N_d} \)
예시:
- \( D_1 = \{1,2,3\},\ D_2 = \{1,2\} \) 일 때
- 조건 \( (D_2 = 1) \) 에 대해 \( m_1 = [0, 0, 0] \) \( m_2 = [1, 0] \)
- 따라서 \( \text{cond} = [0, 0, 0, 1, 0] \)
Generator loss.
훈련 중에, 조건부 생성기(conditional generator)는 어떤 one-hot 이산 벡터 집합 \(\{\hat{d}_1, \dots, \hat{d}_{N_d}\}\)도 자유롭게 생성할 수 있다. 특히, cond 벡터 형태의 조건 \((D_{i^*} = k^*)\)가 주어졌을 때, feed-forward 과정에서는 \(\hat{d}_{i^*}^{(k^*)} = 0\)이 되거나, 다른 값 \(k \neq k^*\)에 대해 \(\hat{d}_{i^*}^{(k)} = 1\)이 되는 것을 막을 수 있는 메커니즘이 없다.
이러한 상황에서, 조건부 생성기가 \(\hat{d}_{i^*} = m_{i^*}\)를 생성하도록 강제하기 위해 제안된 메커니즘은,
\(m_{i^*}\)와 \(\hat{d}_{i^*}\) 사이의 cross-entropy를 배치 내 모든 샘플에 대해 평균 내어 생성기의 손실에 추가하는 것이다.
따라서 훈련이 진행됨에 따라, 생성기는 주어진 \(m_{i^*}\)를 \(\hat{d}_{i^*}\)에 정확히 복사하도록 학습하게 된다.
Training-by-Sampling
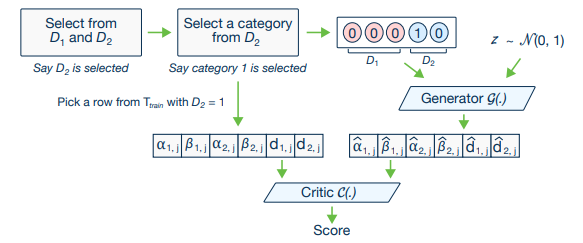
조건부 생성기의 출력은 critic이 학습된 조건부 분포 \(P_G(\text{row} \mid \text{cond})\)와 실제 데이터 분포 \(P(\text{row} \mid \text{cond})\) 간 거리를 평가하는 데 사용된다. critic이 정확한 평가를 하려면 학습 데이터 샘플링과 cond 벡터 구성이 적절해야 하며, 이는 이산형 컬럼의 모든 값을 고르게 탐색하는 데 중요하다.
이를 위해 다음 절차를 따른다:
- \(N_d\)개의 각 이산형 컬럼에 대응하는 0으로 채워진 마스크 벡터 \( m_i = [m_i^{(k)}]_{k=1}^{|D_i|} \) 를 만든다.
- 균등 확률로 이산형 컬럼 \(D_{i^*}\)를 선택한다.
- 선택한 컬럼 \(D_{i^*}\)의 값 범위에 대해 로그 빈도를 확률 질량 함수(PMF)로 만든다. 각 값의 확률 질량은 해당 값이 컬럼에서 등장하는 빈도의 로그값으로 정한다.
- 이 PMF에 따라 값 \(k^*\)를 샘플링하고, 해당 위치를 1로 설정하여 \( m_{i^*}^{(k^*)} = 1 \) 을 만든다.
- 모든 마스크 벡터를 이어붙여 조건 벡터 \( \text{cond} = m_1 \oplus \cdots \oplus m_{i^*} \oplus \cdots \oplus m_{N_d}
\) 를 생성한다.
이렇게 하면 모델이 각 범주를 고르게 탐색하도록 돕는다.
4.4 Network Structure
CTGAN에서는 행(row)의 컬럼들이 국소 구조가 없기 때문에, 생성기와 비평가 모두 완전 연결 신경망(fully-connected network)을 사용해 컬럼 간 모든 상관관계를 학습한다. 생성기와 비평가 모두 두 개의 완전 연결 은닉층을 사용하며, 생성기에는 배치 정규화(batch normalization)와 ReLU, 비평가에는 leaky ReLU와 dropout을 적용한다.
생성기(generator)는 입력 와 조건 벡터 cond를 결합해 다음과 같이 계산된다:
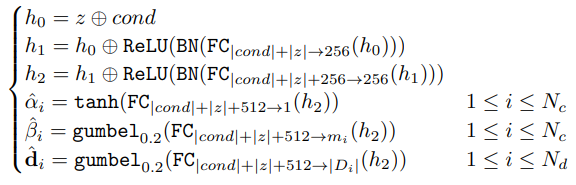
비평가(critic)는 mode collapse를 방지하기 위해 PacGAN 구조를 사용하며, 10개의 샘플을 하나의 배치(pac)로 묶어 처리한다. 비평가의 아키텍처는 다음과 같다:

모델은 gradient penalty가 적용된 WGAN loss로 모델을 학습하며, Adam optimizer를 학습률 \(2 \times 10^{-4}\)로 사용한다.
4.5 TVAE Model
TVAE는 Variational Autoencoder(VAE)를 테이블 데이터에 맞게 변형한 생성 모델이다.
이는 두 개의 신경망
- 인코더: \( q_{\phi}(z_j \mid r_j) \)
- 디코더: \( p_{\theta}(r_j \mid z_j) \)
을 ELBO (Evidence Lower Bound) 손실로 학습한다.
디코더 \( p_{\theta}(r_j \mid z_j) \)는 총 \( 2N_c + N_d \)개의 변수로 구성된 결합 확률분포(joint distribution) 를 출력하며, 각 변수는 다음과 같이 모델링된다:
| 변수 유형 | 기호 | 분포 방식 |
| 연속형 변수 | ( \alpha_{i,j} \) | \( \mathcal{N}(\bar{\alpha}_{i,j}, \delta_i) \) — 평균과 분산이 다른 정규분포 |
| 범주형 변수 1 | \( \beta_{i,j} \) | \( \text{softmax}(\text{FC}_{128 \rightarrow m_i}(h_2)) \) |
| 범주형 변수 2 | \( d_{i,j} \) | \( \text{softmax}(\text{FC}_{128 \rightarrow |D_i|}(h_2)) \) |
디코더는 다음과 같은 다층 퍼셉트론 구조로 구성된다:
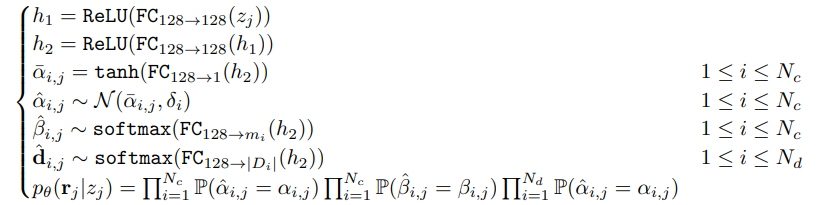
- \( \hat{\alpha}_{i,j} \), \( \hat{\beta}_{i,j} \), \( \hat{d}_{i,j} \)는 확률 변수이며, \( p_{\theta}(r_j \mid z_j) \)는 이들의 결합 분포.
- 네트워크의 가중치 행렬과 \( \delta_i \)는 학습 가능한 파라미터로, 경사 하강법으로 최적화됨.
인코더 \( q_{\phi}(z_j \mid r_j) \)는 기존 VAE와 유사하게 다음과 같이 구성된다:
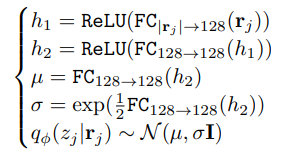
학습은 Adam 옵티마이저(learning rate \(1 \times 10^{-3}\))로 수행된다.